Table of Contents
Class 10 maths ex 7.2 solutions
Class 10 Maths Ex 7.2 solutions : We are providing Class 10 Maths solutions for 7th chapter exercise ex 7.2 class 10 maths solutions “Co-ordinate Geometry” textbook provided by NCERT for CBSE, State boards etc complete exercise solutions with Additional Most Important Questions in our website – online, absolutely for FREE for everyone. No need to do any sign in process, just browse and enjoy all of the Class 10 Maths Chapter 7 exercise 7.2 solutions from us. From the “Class 10 Co-ordinate Geometry”, there are total 3 exercise given in bellow table. Click on the exercise number to browse the complete solutions from ex 7.2 class 10 or the Class 10 Maths Exercise 7.2 solutions ..
Sub-Contents of “Chapter 7 Co-Ordinate Geometry” : There are total 6 sub contents exists in Class 10 maths chapter 7 Co-Ordinate Geometry . We need to study all of the sub-contents first. The Sub Contents are-
| 1. Introduction |
| 2. Distance Formula |
| 3. Section Formula |
| 4. Area of Triangle |
| 5. Summary |
| FROM LATEST UPDATED NCERT SYLLABUS |
Complete Class 10 Maths Exercise 7.2 solutions from latest updated NCERT Syllabus are given bellow:
NOTE: IF YOU FIND THIS PAGE FROM GOOGLE AND SEE SOME CODING LIKE “\cfrac”, Please kindly CLICK HERE to access the original solutions page.
Class 10 Ex 7.2Co-ordinate Geometry Class 10 Question 1 from Class 10 Ex. 7.2Find the co-ordinate of the point which divides (-1,7) and (4,-3) in the ratio 2:3. Solution: Co-ordinate of the point which divides the line joing the points (-1,7) and (4,-3) in the ratio 2:3 is = ( \cfrac{4.2 + (-1).3}{2 + 3} , \cfrac{(-3).2 + 7.3}{2 + 3} ) = ( \cfrac{5}{5} , \cfrac{15}{5} ) = ( 1, 3 ) So, The required point is ( 1, 3 ). Note: If you find this page from google and see some coding like “\cfrac”, please kindly CLICK HERE to see the original page and the solutions. Question 2 from Class 10 Ex 7.2Find the co-ordinate of the points of trisection of the line segment joining ( 4, -1 ) and (-2, -3). Solution: Let P and Q be the points the points of trisection of the line segment joining A( 4, -1 ) and B(-2, -3)
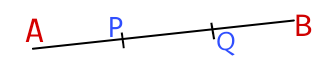
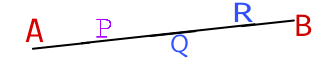
For P, ratio is AP : PB= 1:2 So, co-ordinate of P is =( \cfrac{(-2).1 + 4.2}{1 + 2} , \cfrac{(-3).1 + (-1).2}{1 + 2} ) = ( \cfrac{6}{3} , \cfrac{-5}{3} ) = ( 2 , – \cfrac{5}{3} ) For Q point ratio is, AQ : QB = 2 : 1 So, co-ordinate of Q is = ( \cfrac{(-2).2 + 4.1}{2 + 1} , \cfrac{(-3).2 + (-1).1}{2 + 1} ) = ( \cfrac{0}{3} , \cfrac{-7}{3} ) = ( 0, – \cfrac{7}{3} ) Question 3 from class 10 Ex 7.2Find the ratio in which the line segment joining the points ( -3, 10 ) and (6,-8) is divided by (-1,6) Solution: Let the ratio be m:n So, Co-ordinate of the point which intersect (-3,10) and (6,-8) in m:n ratio is = (-1,6) ⇒ ( \cfrac{6m + (-3)n}{m+n} , \cfrac{(-8)m + 10n}{m+n} ) = ( -1, 6 ) Therefore, \cfrac{6m -3n}{m+n} = -1 ⇒ 6m – 3n = -m -n ⇒ 7m = 2n OR \cfrac{m}{n} = \cfrac{2}{7} So, m : n = 2 : 7 Hence, Required ratio is 2 : 7 Question 5 from Class 10 Ex 7.2Find the ratio in which the line segment joining A( 1, -5 ) and B( -4, 5 ) is divided by the X axis. Also find the co-ordinate of the point of division. Solution: Let the point P( x, 0 ) which is on x-axis, divides the line joining A( 1, -5 ) and B( -4, 5 ) in m:n ratio. So, ( \cfrac{-4.m + 1.n}{m+n} , \cfrac{5.m + (-5).n}{m+n} ) = ( x, 0 ) Hence, \cfrac{-4.m + 1.n}{m+n} = x ————(i) and \cfrac{5.m -5.n}{m+n} = 0 ⇒ 5m – 5n = 0 ⇒ 5m = 5n Hence m : n = 5 : 5 = 1 : 1 Now, From equation (i), by putting m = 1 & n = 1 we get, \cfrac{-4.1 + 1.1}{1+1} = x ⇒ x = \cfrac{-3}{2} Hence, Required co-ordinate of the point on the x axis is (0, \cfrac{-3}{2} ) and this point divides the given line in 1 : 1 ratio. Question 6 from class 10 Ex 7.2If ( 1, 2 ), ( 4, y ), ( x, 6 ) and ( 3, 5 ) are the vertices of a parallelogram taken in order, find x and y. Solution: The given points ( 1, 2 ), ( 4, y ), ( x, 6 ) and ( 3, 5 ) are the vertices of a parallelogram taken in order. We know that, the diagonals of a parallelogram bisects each other. Which means, mid points of the diagonals are same. So, Mid point of the line joining (1,2) and (x,6) = Mid point of the line joining (4,y) and (3,5) ⇒( \cfrac{1+x}{2} , \cfrac{2+6}{2} ) = ( \cfrac{4+3}{2} , \cfrac{y+5}{2} ) Hence, \cfrac{1+x}{2}[/latex ] = [latex]\cfrac{7}{2} ⇒ 2 + 2x = 14 ⇒ 2x = 12 ⇒ x = 6 And, \cfrac{2+6}{2} = \cfrac{y+5}{2} ⇒2y + 10 = 16 ⇒ 2y = 6 ⇒ y = 3 Hence, value of x = 6 and y = 3 Question 7 from class 10 Ex 7.2Find the Co-ordinate of the point A where AB is the diameter of a circle whose centre is (2, -3) and B is (1,4). Solution: Let, (x,y) be the Co-ordinate of the point A. We know, centre is the mid point of diameter. So, Mid point of (x,y) and (1,4) = (2,-3) ⇒ ( \cfrac{x + 1}{2} , \cfrac{y + 4}{2} = ( 2, -3) So, \cfrac{x + 1}{2} = 2 ⇒ x + 1 = 4 ⇒ x = 3 And, \cfrac{y + 4}{2} = -3 ⇒ y + 4 = -6 ⇒ y = -10 Hence, required value of x = 3 & y = -10 Question 8 from Class 10 Ex 7.2If A and B are (-2, -2) and (2, -4) respectively, find the Co-ordinate of P such that AP = \cfrac{3}{7}AB and P lies on the line segment AB Solution: Here, AP = \cfrac{3}{7}AB Clearly, PB = \cfrac{4}{7}AB Hence, AP : PB = 3 : 4 So, Co-ordinate of the point which bisects A( -2, -2 ) and B( 2, -4 ) at 3 : 4 is = ( \cfrac{2.3 + (-2).4}{3 + 4} , \cfrac{(-4).3 + (-2).4}{3 + 4} ) = ( \cfrac{-2}{7} , \cfrac{-20}{7} ) Hence, required Co-ordinate of the point A( \cfrac{-2}{7} , \cfrac{-20}{7} ) Question 9 from Class 10 Ex 7.2Find the Co-ordinate of the points which divides the line segment joining A( -2, 2 ) and B( 2, 8 ) into four equal parts. Solution: Let the points be P, Q, R be the points which intersects the line AB into four parts.
For point P, AP: PB = 1 : 3 So, Co-ordinate of P is = ( \cfrac{2.1 + (-2).3}{1 + 3} , \cfrac{8.1 + 2.3}{1 + 3} ) = ( \cfrac{-4}{4} , \cfrac{14}{4} ) = ( -1 , \cfrac{7}{2} ) For point Q, AQ : QB = 2 : 2 So, Co-ordinate of Q is = ( \cfrac{2.2 + (-2).2}{2 + 2} , \cfrac{8.2 + 2.2}{2 + 2} ) = ( \cfrac{0}{4} , \cfrac{20}{4} ) = ( 0 , 5 ) For Point R, AR : RB = 3 : 1 So, Co-ordinate of R is = ( \cfrac{2.3 + (-2).1}{3 + 1} , \cfrac{8.3 + 2.1}{3 + 1} ) = ( \cfrac{4}{4} , \cfrac{26}{4} ) = ( 1 , \cfrac{13}{2} ) Therefore, The required points are ( -1 , \cfrac{7}{2} ) , ( 0, 5 ) and ( 1 , \cfrac{13}{2} ) respectively. Question 10 from class 10 Ex 7.2Find the area of a rhombus if its vertices are ( 3, 0), ( 4, 5), ( -1, 4) and ( -2, -1) taken in order. Solution: Let the four points be A( 3, 0), B( 4, 5), C( -1, 4) and D( -2, -1) Hence, AC = \sqrt{ (3 - (-1))^2 + (0 - 4)^2} = \sqrt{ 4^2 + 4^2} = 4 \sqrt{2} BD = \sqrt{ (4 - (-2))^2 + (5 - (-1))^2} = \sqrt{ 6^2 + 6^2} = 6 \sqrt{2} Therefore, Area of the Rhombus is = \cfrac{1}{2} × AC × BD = \cfrac{1}{2} × 4 \sqrt{2} × 6 \sqrt{2} = 24 sq. units Hence, Required area of the Rhombus is 24 Sq. units. |
Formulae Used in Class 10 maths Ex 7.2
Below, we have discussed the two Special formulae used in this exercise.
Section Formula
The formula, using which, we can find the Co-ordinate of a point, which intersects any line in some particular ratio, is known as the section Formula in Co-ordinate Geometry. It’s one of the most interesting and most important formula from Co-ordinate Geometry for class 10. The formula is given bellow:
Let us consider any two points A(x1, y1) and B(x2, y2). Let us take that any point P intersects the line joining A and B in a particular ratio m : n. Then the Co-ordinate of the point P is-
| ( \cfrac{m.x2 + n.x1}{m + n} , \cfrac{m.y2 + n.y1}{m + n} ) |
So, using this formula, we can get the Co-ordinate of the intersected point.
Mid Point Formula
This formula is just a sub-formula or a special case of section Formula. Using this, we can get the midle point of any line joining two Co-ordinate points.
Let (x1, y1) and (x2, y2) be any two points. Then the midle point of the line, joining these two points, is given by –
| ( \cfrac{x1 + x2}{2} , \cfrac{y1 + y2}{2} ) |
Some Co-ordinate Geometry G.K.
Some most important facts of Co-Ordinate Geometry are given bellow, must remember these as these are also important for any other competitive exams and interviews–
- Co-ordinate of origin is (0, 0)
- Co-ordinate of a point on X-axis is (x, 0)
- Co-ordinate of a point on Y-axis is (0, y)
- Distant from X-axis to (x, y) point is = y unites
- Distant from Y-axis to (x, y) point is = x unites
- Co-ordinate of a point in 1st Quadrant = (x, y)
- Co-ordinate of a point in 2st Quadrant = (-x, y)
- Co-ordinate of a point in 3st Quadrant = (-x, -y)
- Co-ordinate of a point in 4st Quadrant = (x, -y)
- Equation of a X- axis is: y = 0
- Equation of a Y- axis is: x = 0
- Equation of a line parallel to X-axis: y = a
- Equation of a line parallel to Y-axis: x = b
NCERT SOLUTIONS FROM CLASS 10 MATHS :
We are providing complete Class 10 Maths Solution . You can get complete and updated solution from our website. Please click on your prefered chapter bellow from NCERT CLASS 10 MATHS and see the solutions. You can get complete ncert solutions for class 10 maths from here.
| 1 Chapter 1 Real Numbers |
| 2 Chapter 2 Polynomials |
| 3 Chapter 3 Pair of Linear Equations in Two Variables |
| 4 Chapter 4 Quadratic Equations |
| 5 Chapter 5 Arithmetic Progressions |
| 6 Chapter 6 Triangles |
| 7 Chapter 7 Co-ordinate Geometry |
| 8 Chapter 8 Introduction to trigonometry |
| 9 Chapter 9 Application of Trigonometry |
| 10 Chapter 10 Circle |
| 11 Chapter 11 Constructions |
| 12 Chapter 12 Area Related to Circles |
| 13 Chapter 13 Surface area and volumes |
| 14 Chapter 14 Statistics |
| 15 Chapter 15 Probability |
Additional Links:
- THAN vs THEN – Difference Between Than and Then with Examples
- WHAT IS TRIGONOMETRY? (Trigonometry Complete Course – Click Here)
- Assam HSLC 2020 Results date, all working links to check results online.
- SEBA HSLC Question Paper Collection.
- Irrigation ASSAM 2020 Result, Final Merit List PDF Download
- CTET OFFICIAL WEBSITE CLICK HERE
Class 10 Maths Exercise 7.2 solutions