Trigonometry Formulas Table and List

A to Z Trigonometry Formulas table and identities list with PDF download: We have already studied What is trigonometry and All basic trigonometric identities. Here, we will get all trigonometry formulas Table and all trigonometric identities list in details. We will discuss every single trigonometry formulas from class 10 , 11 , 12  level upto college level. We will study from basic trigonometric identities to inverse trigonometry Formulas also.

Remember, Plural of Formula is Formulae, Not Formulas. We are using “formulas” instead of “formulae” for some third party reason’s only.

 

Before we starting to learn all trigonometry formulas table and list , please read the definitions and all basic identities of trigonometry by going into the bellow links:

Trigonometry definitions

Basic Trigonometric Identities

PLEASE NOTE: If you find this page from Google and see some coding like “\cfrac” instead, please CLICK HERE to access the original formulae bank page.

---

BASIC Trigonometry Formulas Table FORMULAE

Basic Trigonometric Identities For Class 10, 11 with Proof (Part 2)

 

Below have have again discussed the basic trigonometry formulas table briefly. Firstly, Remember this trigonometric table to clear the conecpets and main definitions of all the trigonometric ratios:

Sin	Perpendicular / hypotenuse	P / H
Cosec	hypotenuse / Perpendicular	H / P
Tan	Perpendicular / Base	P / B
Cot	Base / Perpendicular	B / P
Cos	Base / hypotenuse	B / H
Sec	hypotenuse / Base	H / B

 

TRIGONOMETRY FORMULAS LIST – 2

From the above list, we have seen that, three trigonometric ratios are opposite of the other three trigonometric ratios. Specially, sin and cosec, tan and cot, cos and sec are completely opposite to each other. That is why, we can get the following trigonometric identities list from the above table.

1	sinA.cosecA = 1	sinA = \cfrac{1}{cosecA}	cosecA = \cfrac{1}{sinA}
2	tanA.cotA = 1	tanA = \cfrac{1}{cotA}	cotA = \cfrac{1}{tanA}
3	cosA.secA = 1	cosA = \cfrac{1}{secA}	secA = \cfrac{1}{cosA}

 

PLEASE NOTE: If you find this page from Google and see some coding like “\cfrac” instead, please CLICK HERE to access the original formulae bank page.

Some Important Trigonometry Notes

• Numerical Values of sinθ and cosθ cannt be greater than 1
• The maximum and minimum numerical values of sinθ and cosθ are 1 and -1.
• Sqaure of sinθ and cosθ are always equal or less than 1.
• Square of secθ and cosecθ are always equal or greater than 1.
• tanθ and cotθ may have any numerical values.

TRIGONOMETRY FORMULAS LIST – 3

As like as List – 2, from the first list, we can get the bellow trigonometry ratio formulas list, that you must have to noted and remembered, if you want to study trigonometry. These trigonometric identities are most important for Trigonometric formulas for class 10.

1	tanA = \cfrac{sinA}{cosA}	cotA = \cfrac{cosA}{sinA}
2	tanA = \cfrac{secA}{cosecA}	cotA = \cfrac{cosecA}{secA}

 

3 THREE SPECIAL TRIGONOMETRY FORMULA

The bellow three trigonometric formulas are very special. These are also most important for Trigonometry Formulas for any interview  specially ssc , amry, bank, railways etc and also for Trigonometry formulas for class 10 11 , 12 and higher classes.. The three very special formulae are –

(i) Sin²A + Cos²A = 1

(ii) 1 + Tan²A = Sec²A

(iii) 1 + Cot²A = Cosec²A

From these three formulae, we can get some sub-formulae as given bellow-

From the first trigonometric formula :

        (a) sin²A = 1 – cos²A

        (b) sinA = \sqrt{1 - cos²A}

        (c) cos²A = 1 – sin²A

        (d) cosA = \sqrt{1 - sin²A}

From the Second Trigonometric Formula , We get-

        (a) Sec²A – Tan²A = 1

        (b) SecA = \sqrt{1 + Tan²A}

        (c) Tan²A = Sec²A – 1

        (d) TanA = \sqrt{Sec²A - 1}

From the third trigonometric formulae, we get

        (a) Cosec²A – Cot²A = 1

        (b) CosecA = \sqrt{1 + Cot²A}

        (c) Cot²A = Cosec²A – 1

        (d) CotA = \sqrt{Cosec²A - 1}

---

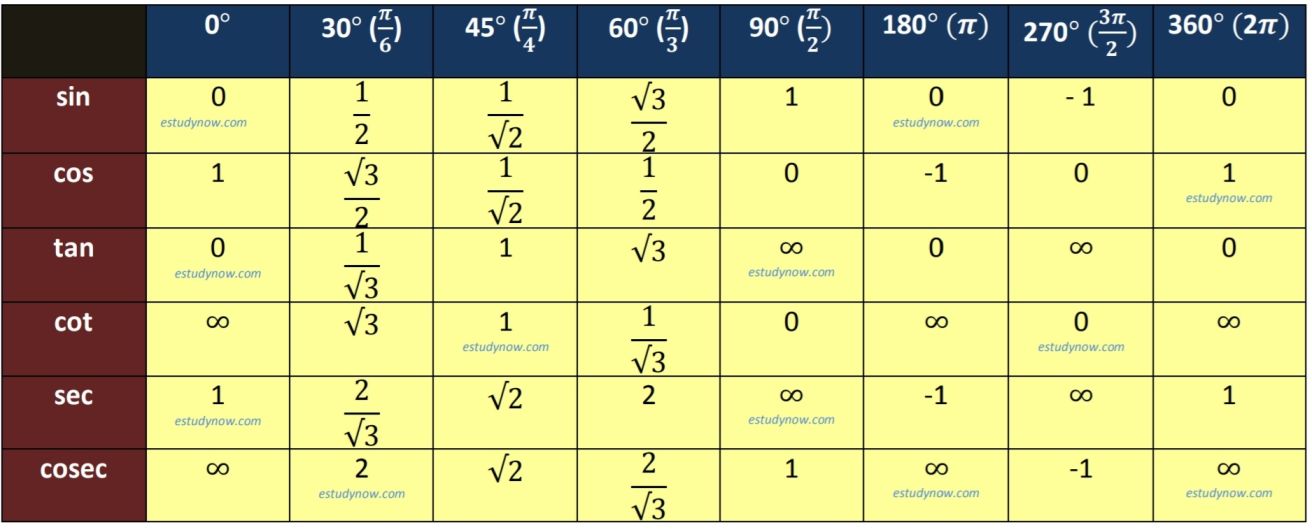
Trigonometry Formulas TABLE :

Now, we discuss about the value of sin, cos, tan, cot, sec and cosec at some particular given values. You must have to remember the following table as it is one of the most important table for high school level to any degree and also for any competative exams and interview like ssc, army, aif etc..

Negative Angle and Specific Angle Trigonometry Formulas

Here are some most important trigonometric formulas given bellow for negative angles and at some specific types of angle. These formulae are trigonometry class 10 high school level. Study them –

(a) sin(-θ) = -sinθ

     cos(-θ) = cosθ

     tan(-θ) = -tanθ

(b) sin(90º – A) = cosA,     cos(90º – A) = sinA

     tan(90º – A) = cotA,     cot(90º – A) = tanA

     sec(90º – A) = cosecA,  cosec(90º – A) = secA

(c) sin(180º – A) = sinA,    sin(180º + A) = – sinA

     cos(180º – A) = – cosA, cos(180º + A) = – cosA

     tan(180º – A) = – tanA, tan(180º + A) = tanA

After all, We can get the following table as like as the above results.

 

---

TRIGONOMETRY Addition Formulas List – 5

We have listed some trigonometric formulas for class 11 , 12 and higher classes belllow. These are also important for Classs 10 trigonometry . Let A,B and C be any two angle. Then, we can get the following trigonometry formulas, where we have added cos(a+b) , sin(a+b) , tan(a+b) , cot (a+b) formulae –

• Sin(A + B) = SinA.CosB + CosA.SinB
• Cos(A + B) = SinA.CosB – CosA.SinB
• Tan(A + B) = \cfrac{TanA + TanB}{1 - TanA.tanB}
• Cot(A + B) = \cfrac{CotA.Cotb - 1}{CotA + CotB}

• sin(A + B + C) = sinA.cosB.cosC + sinB.cosA.cosC + sinC.cosA.cosB – sinA.sinB.sinC
• cos(A + B + C) = coaA.cosB.cosC – cosA.sinB.sinC – cosB.sinA.sinC – cosC.sinA.sinB
• tan(A + B + C) = \cfrac{tanA + tanB + tanC - tanA.tanB.tanC}{1 - tanA.tanB - tanB.tanC - tanA.tanC}

TRIGONOMETRY SUBSTRACTION FORMULAS

Let A and B be any two angle. Then, we can get the following trigonometry substraction formulas, where we have added the sin(a-b), cos(a-b), tan(a-b). cot(a-b) formulae –

• Sin(A – B) = SinA.CosB – CosA.SinB
• Cos(A – B) = SinA.CosB + CosA.SinB
• Tan(A – B) = \cfrac{TanA - TanB}{1 + TanA.tanB}
• Cot(A – B) = \cfrac{CotA.Cotb + 1}{CotA - CotB}

---

TRIGONOMETRY PRODUCT FORMULAS

Let A and B be any two angle. than –

• 2sinA.cosB = sin(A + B) + sin(A – B)
• 2cosA.sinB = sin(A + B) – sin(A – B)
• 2cosA.cosB = cos(A + B) + cos (A – B)
• -2sinA.sinB = cos(A + B) – cos (A – B)

TRIGONOMETRY SUM Product Formulae

Let us consider any two angle X and Y, then we can get the following formulas –

• cosX + cosY = 2cos \cfrac{X + Y}{2}.cos \cfrac{X - Y}{2}
• cosX – cosY = -2sin \cfrac{X + Y}{2}. sin \cfrac{X - Y}{2}
• sinX + sinY = 2sin \cfrac{X + Y}{2}. cos \cfrac{X - Y}{2}
• sinX – sinY = 2cos \cfrac{X + Y}{2}. sin \cfrac{X - Y}{2}

Most Important 2 Special Trigonometry Formula

Two most important trigonometric identities for any two angle A and B are given bellow:

A. Sin(A + B).Sin(A – B) = sin²A – sin²B

                                    = cos²B – cos²A

B. Cos(A + B).Cos(A – B) = cos²A- sin²B

                                    = cos²B – sin²A

---

Trigonometry Double Angle Formulas:

For any angle A, the double angle formulae are given bellow-

♦ sin2A = 2sinA.cosB = \cfrac{2tanA}{1 + tanA}

♦ cos2A = cos²A- sin²A

            = 2cos²A – 1

            = 1 – 2sin²A

            = \cfrac{1 - tan²A}{1 + tan²A}

♦ tan2A =  \cfrac{2tanA}{1 - tan²A}

Trigonometry Triple Angle Formula

» sin3A = 3.sinA – 4.sin³A

» cos3A = 4.cos³A – 3.cosA

» tan3A = \cfrac{3tanA - tan³A}{1 - 3tan²A}

Trigonometry Half Angle Identities

» sinθ = 2.sin \frac θ 2 .cos \frac θ 2

» cosθ = cos² \frac θ 2 – sin² \frac θ 2

           = 2cos² \frac θ 2 – 1

           = 1 – 2sin² \frac θ 2

» tanθ = \cfrac{2tan \frac θ2}{1 - tan² \frac θ2 }

» 1 – cosθ = 2sin² \frac θ 2

» 1 + cosθ = 2cos² \frac θ 2

---

Trigonometric Equations General Solution Formulae

PLEASE NOTE: If you find this page from Google and see some coding like “\cfrac” instead, please CLICK HERE to access the original formulae bank page.

• If sinθ = 0 , then θ = nπ
• If cosθ = 0 , then θ = (2n + 1)\cfrac{π}{2}
• If tanθ = 0 , then θ = nπ
• If cotθ = 0 , then θ = (2n + 1)\cfrac{π}{2}
• If sinθ = 1 , then θ = (4n + 1)\cfrac{π}{2}
• If cosθ = 1 , then θ = 2nπ
• If tanθ = 1 , then θ = (4n + 1)\cfrac{π}{4}
• If cotθ = 1 , then θ = (2n + 1)\cfrac{π}{4}
• If sinθ = – 1 , then θ = (4n – 1)\cfrac{π}{2}
• If cosθ = – 1 , then θ = (2n + 1)π
• If tanθ = – 1 , then θ = (4n – 1)\cfrac{π}{4}
• If cotθ = – 1 , then θ = (4n – 1)\cfrac{π}{4}
• If sinθ = sinα, then θ = nπ + (-1)^n α
• If cosθ = cosα, then θ = 2nπ ± α
• If tanθ = tanα, then θ = nπ + α
• If sinθ = – sinα, then θ = nπ + (-1)^n+1 α
• If cosθ = – cosα, then θ = (2nπ + 1)π – α
• If tanθ = – tanα, then θ = nπ – α
• If sin^2θ = sin^2α , then θ = nπ ± α
• If cos^2θ = cos^2α , then θ = nπ ± α
• If tan^2θ = tan^2α , then θ = nπ ± α

Inverse Trigonometry Formula

Inverse Trigonometric formulas for higher classes are giver bellow:

• sin-¹x + cos-¹x = \frac 1 2π
• tan-¹x + cot-¹x = \frac 1 2π
• sec-¹x + cosec-¹x = \frac 1 2π
• tan-¹x + tan-¹y = tan-¹ \cfrac {x + y}{1 - xy}
• tan-¹x – tan-¹y = tan-¹ \cfrac {x - y}{1 + xy}
• tan-¹x + tan-¹y + tan-¹z = tan-¹ \cfrac {x + y +z - xyz}{1 - xy - yz - zx}

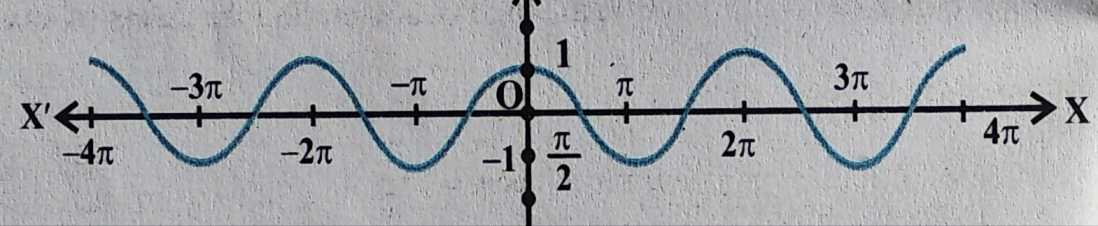
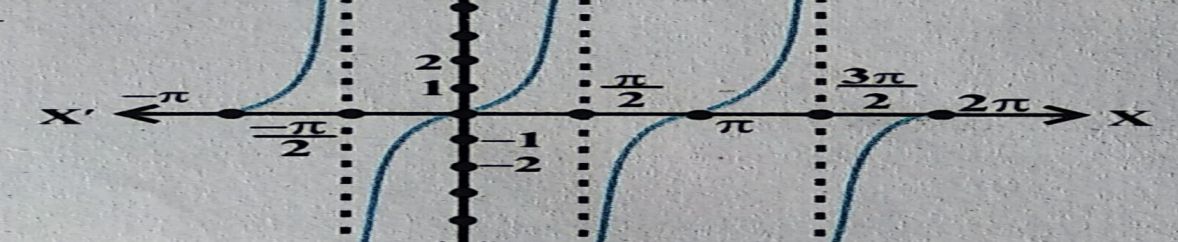
Trigonometric Ratios Graphs

We can draw graph for each of the six trigonometric ratios in co-ordinate planes, specially in X and Y plane. Hereby, we have also included all the six graphs for each of the six trigonometric ratios bellow. These graphs are most important for higher classes in trigonometry fucntions analysis. Study them carefully or note somewhere.

Sin Graph for y = sinx

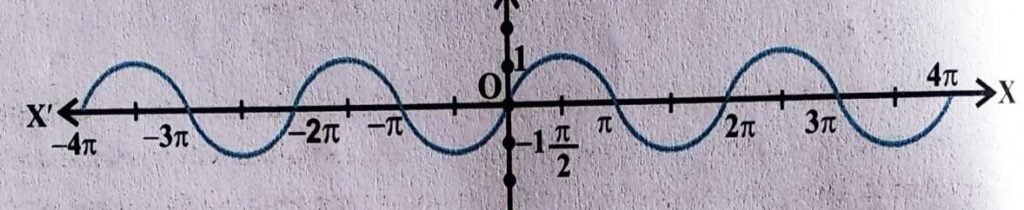
Cos Graph for y = cosx

Tan Graph for y = tanx

Cot Graph for y = cotx

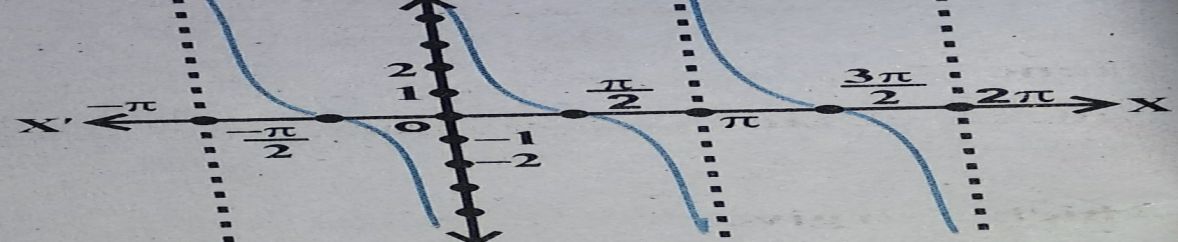
Sec Graph for y = secx

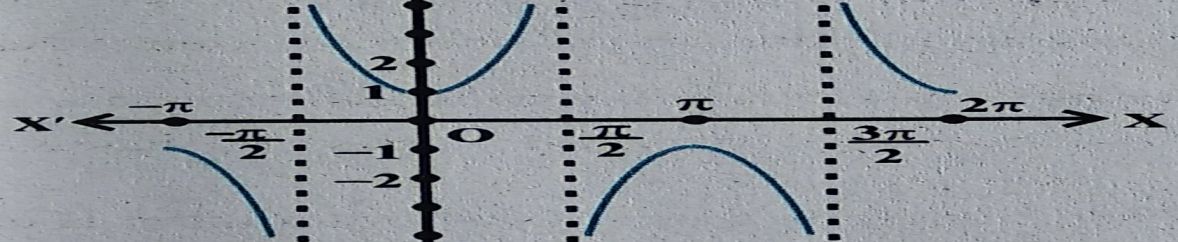
Cosec Graph for y = cosecx

Source : CLICK HERE!

---

Trigonometry for Complex Number

A number that can be expressed in the form a + ib is a complex number. Here, “i” denotes iota having value √-1 

(cosθ ± isinθ)^n = cos nθ ± isin nθ

Series for Trigonometric Ratios

Every trigonometric ratios can be expressed as a series of some numbers as follows:

◊ sin a = a – \cfrac{a³}{3!} + \cfrac{a^5}{5!} – ……∝

◊ cos a = 1 – \cfrac{a²}{2!} + \cfrac{a^4}{4!} – ……∝

◊ tan a = a + \cfrac{1}{3} a^3 + \cfrac{2}{15} a^5 + …….∝

FINAL WORDS

We have just learnt only a part of trigonometric formulae. There are still a big trigonometry chart exsists to be studied. But, for upto approx higher secondary or degree level, approximately, these are enough. We can also get some beautifull Trigonometric graph for each trigonometric ratios as given. 

As trigonometry is one of the most interesting content of Mathematics, one can access the instant and free formulae list from this page through internat by just searching as “a to z trigonometry formulas estudynow”. Such a magical content, surely, these notes will help anyone who need it. Thanks for enjoying these all. If you want to learn more about trigonometry, simply Click Here now.

DOWNLOAD Trigonometry Formulas PDF

If you want to access this page while offline too, simply download the pdf file of this page from bellow section. After downloading this trigonometric formulas list pdf, open the file using any pdf reader and access the page while you are offline too. See you again!

DOWNLOAD PDF

Download only table

Frequently Asked Questions and Answer

Q. what is cos(a+b) ? Answer: cosa.cosb – sina.sinb

 

Q. For any angle A, sinA = 7, is this possible? Answer: No! Value of sinA never be greater than 1.

 

Q. What is trigonometry? Answer: Well! Click Here to know complete answer. https://estudynow.com/what-is-trigonometry/

 

Q. What are trigonometry formulas table ? Answer: All the formulae, A to Z are given with discriptions– Go Here!

 

You have studied All Trigonometry Formulas Table