Pipes A and B can fill a tank in 8 and 24 hours respectively. Pipe C can empty it in 12 hours. If the three pipes are opened together, then the tank will be fill in –

Hindi: पाइप A और B क्रमशः 8 और 24 घंटे में एक टैंक भर सकते हैं। पाइप C इसे 12 घंटे में खाली कर सकता है। यदि तीन पाइपों को एक साथ खोला जाता है, तो टैंक को भर दिया जाएगा –

A. 18 Hours

B. 6 Hours

C. 24 Hours

D. 12 Hours

 

Solutions:

Method – 1

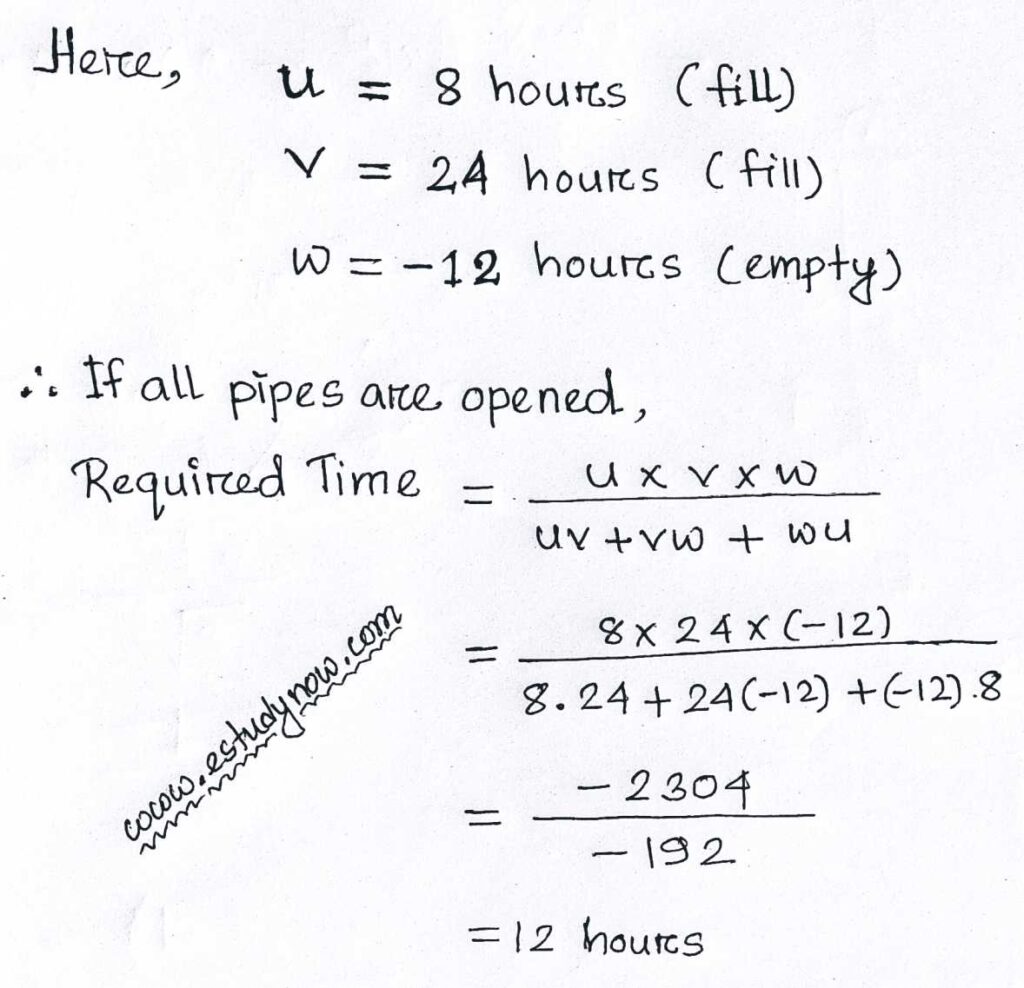
Method – 2

Pipe A can fill in 1 hour = 1/8 

Pipe B can fill in 1 hour = 1/24

Pipe C can empty in 1 hour = – 1/12

So, If all 3 Pipes are opened

Time = 1/8 + 1/24 – 1/12 = 2/24

           = 1/12 

So, Required Moment = 12 Hours

---

Main Shortcut Formula:

If any three different sources, suppose A , B & C complete any work in different moments, say U, V and W. Then we can easily find the required time, that is needed to complete the work by the three sources together. 

Here is the main formula:

If U, V & W be the three different moments, then,

Required Time = ( U × V × W ) ÷ ( UV + VW + WU)

We have solve the problem using this formula as Method – 1.

---

All Confusion Clear?

Do you have any more problems, Questions?

Please Ask me in Comments now.