Pipes A and B can fill a tank in 8 and 24 hours respectively. Pipe C can empty it in 12 hours. If the three pipes are opened together, then the tank will be fill in –
Hindi: पाइप A और B क्रमशः 8 और 24 घंटे में एक टैंक भर सकते हैं। पाइप C इसे 12 घंटे में खाली कर सकता है। यदि तीन पाइपों को एक साथ खोला जाता है, तो टैंक को भर दिया जाएगा –
| A. 18 Hours |
| B. 6 Hours |
| C. 24 Hours |
| D. 12 Hours |
Solutions:
Method – 1
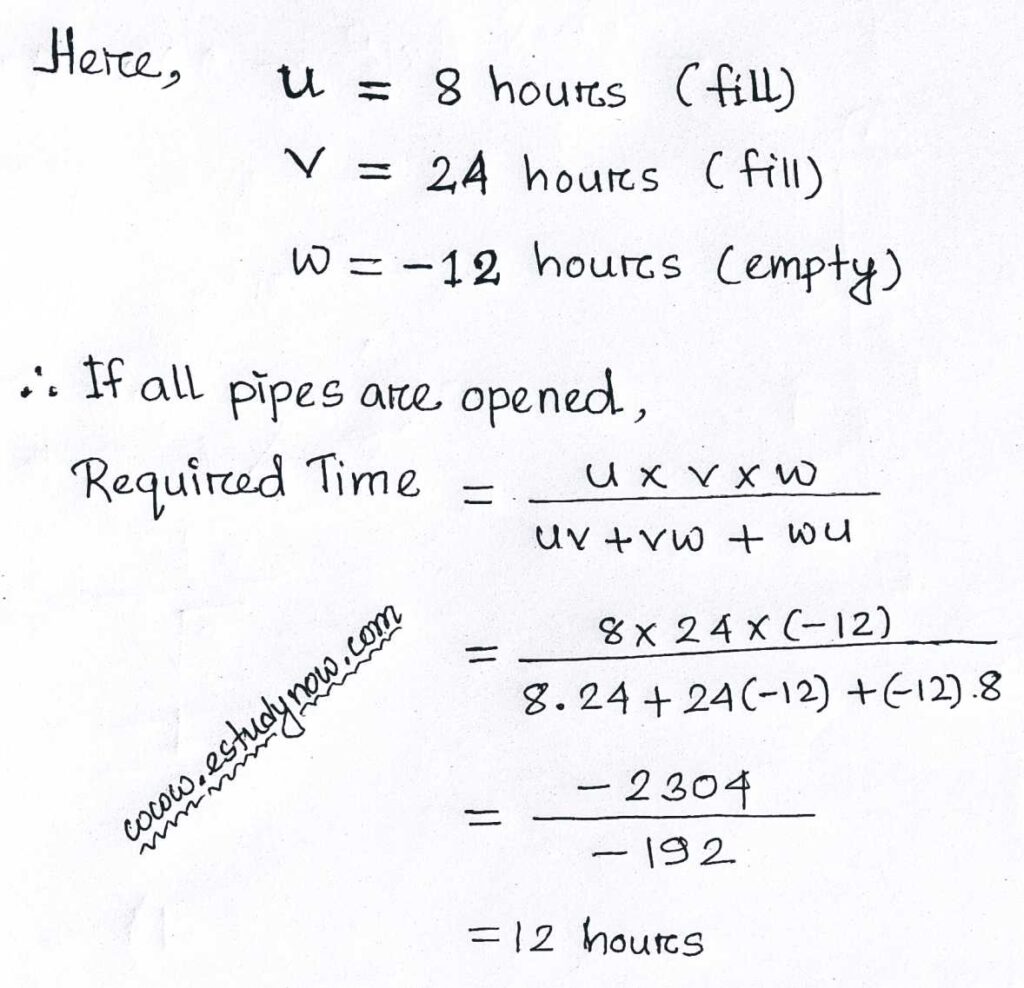
Method – 2
Pipe A can fill in 1 hour = 1/8
Pipe B can fill in 1 hour = 1/24
Pipe C can empty in 1 hour = – 1/12
So, If all 3 Pipes are opened
Time = 1/8 + 1/24 – 1/12 = 2/24
= 1/12
So, Required Moment = 12 Hours
Main Shortcut Formula:
If any three different sources, suppose A , B & C complete any work in different moments, say U, V and W. Then we can easily find the required time, that is needed to complete the work by the three sources together.
Here is the main formula:
If U, V & W be the three different moments, then,
Required Time = ( U × V × W ) ÷ ( UV + VW + WU)
We have solve the problem using this formula as Method – 1.
All Confusion Clear?
Do you have any more problems, Questions?
Please Ask me in Comments now.
Thanks
